[알고리즘] LIS(Longest Increasing Sequence)

최장 증가 부분 수열 (LIS, Longest Increasing Sequence)

---

최장 증가 부분 수열(LIS) 란?

어떤 임의의 수열이 주어질 때, 이 수열에서 몇 개의 수들을 제거하여 부분 수열을 만들 수 있다. 이 때 만들어진 부분 수열 중 오름차순으로 정렬된 가장 긴 수열을 최장 증가 부분 수열이라 한다.

예를 들어,
[6,2,5,1,7,4,8,3] 라는 수열이 존재하는 경우 LIS는 [2,5,7,8] 이 된다.
[2,5], [2,7] 등 증가하는 부분 수열은 많지만 그 중에서 가장 긴 것이 [2,5,7,8] 이기 때문이다.

LIS(최장 증가 부분 수열)의 길이를 구하는 방법에는 두 가지가 있다.
(1) DP(Dynamic Programing, 동적 계획법) - O(N^2) 알고리즘
(2) Lower Bound(Binary Search 이용 한 풀이 방식) - O(NlogN) 알고리즘


* DP(Dynamic Programing, 동적 계획법)
하나의 큰 문제를 여러 개의 작은 문제로 나누어서 그 결과를 저장(메모이제이션, Memoization)하여 다시 큰 문제를 해결할 때 사용하는 것으로 특정한 알고리즘이 아닌 하나의 문제해결 패러다임으로 볼 수 있다.

* Lower Bound
어떠한 정렬된 배열 arr에서 어떠한 값 val의 Lower Bound란 arr을 정렬된 상태로 유지하면서 val이 삽입될 수 있는 위치들 중 가장 인덱스가 작은 것을 의미한다.

예를 들어,
[1,3,3,6,7] 라는 배열에서 1의 Lower Bound 는 0이고, 3의 Lower Bound는 1 이며, 5의 Lower Bound는 2이다.

Lower Bound는 이진 탐색(Binary Search)을 통해 logN 시간에 구할 수 있다.


* 이분 탐색(Binary Search)?
이진 탐색이란 데이터가 정렬되어 있는 배열에서 특정한 값을 찾아내는 알고리즘이다. X가 중간 값보다 작으면 중간 값을 기준으로 좌측의 데이터 들을 대상으로, X가 중간 값보다 크면 배열의 우측을 대상으로 다시 탐색한다. 동일한 방법으로 다시 중간의 값과 X를 비교하며 해당 값을 찾을 때까지 이 과정을 반복하게 된다.

* 참고

[알고리즘] 이진 탐색(Binary Search, 이분 탐색)

---

코드(Python) - dp 방식 풀이

x = int(input())

arr = list(map(int, input().split()))

dp = [1 for i in range(x)]

for i in range(x):
    for j in range(i):
        if arr[i] > arr[j]:
            dp[i] = max(dp[i], dp[j]+1)

(1) 수열의 길이를 담은 dp 배열을 1로 초기화(dp의 Memoization) 해준다.
(2) arr(수열)에서 인덱스를 한 칸씩(i+=1) 늘려가면서 확인한다.
(3) 내부 반복문으로 i 보다 작은 인덱스들을 하나씩 살펴보며 arr[i] > arr[j] 인 경우, dp[i] 값을 업데이트 해준다.
(4) i 번째 인덱스에서 끝나는 최장 증가 부분 수열의 마지막에 dp[j]를 추가했을 때의 LIS 길이와 추가하지 않고 기존의 dp[i] 값을 비교하여 둘 중 더 큰 값으로 dp[i] 값을 업데이트 해준다.


※ 추가 설명
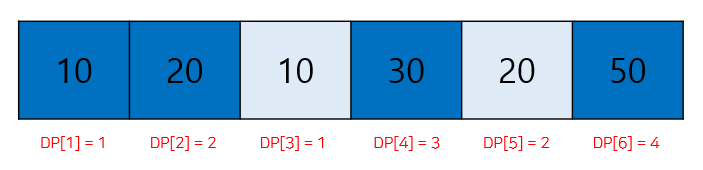
입력 받은 arr 배열이 [10, 20, 10, 30, 20, 50] 라고 할 때 DP 배열은 다음 그림과 같이 [1,2,1,3,2,4]가 될 것이며 LIS의 길이는 DP 배열 값들 중 가장 큰 값이 될 것이기 때문에 4 가 될 것이다.

---

코드(C++, Python) - 이분 탐색 풀이

DP 를 이용하여 LIS 문제를 해결하려는 경우 전체 시간 복잡도가 O(N^2) 이므로 비 효율적이다. 이러한 시간 복잡도를 개선하기 위하여 Lower Bound 방식으로 문제를 풀이할 수 있으며 이진 탐색을 통해 풀이되므로 전체 시간 복잡도 O(NlogN)이 된다.

이 알고리즘은 다음과 같이 리스트 lis 를 업데이트 하며 동작한다.
lis[i]는 길이 i인 증가하는 부분 수열을 만들 수 있는 마지막 원소 중 가장 작은 값을 의미하며 따라서 lis 의 크기가 곧 현재까지 만들 수 있는 lis의 길이이며, 처음에는 빈 리스트로 시작하게 된다.

(1) lis 가 비어 있거나 현재 lis 의 마지막 원소보다 var 이 더 큰 경우 lis 뒤에 var을 추가해 준다. 지금까지 만들 수 있는 가장 긴 증가하는 부분 수열의 마지막 원소보다 var이 더 크기 때문에 var을 마지막으로 만들 수 있는 LIS의 길이는 현재 lis의 길이 + 1 이기 때문이다.
(2) 그렇지 않을 경우 lis 배열에서 var의 Lower Bound를 찾아서 그 자리를 var 로 바꾼다.

따라서, lis 의 크기인 3이 이 수열에서 LIS 길이가 된다. Lower Bound 로 LIS를 구하려는 경우 최장 길이만 구할 수 있다.

추가적인 예를 들어 Lower Bound로 LIS의 길이를 구하는 것을 좀 더 이해해 보자면
[3,5,2,6,1] 배열이 존재하는 경우
lis = [3]
lis = [3,5]
lis = [2,5]
lis = [2,5,6]
lis = [1,5,6]

lis의 마지막 값보다 큰 경우 바로 뒤에 붙게 되고 작은 경우 단순 교체가 되므로 길이에는 영향을 주지 않는다.
따라서 실제 LIS는 [3,5,6] 이지만 단순히 길이를 구하는 목적이라면 이는 답에 영향을 주지 않게 된다.



[C++]

#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <vector>
#include <deque>

using namespace std;

int n;
int arr[40001];
int lis[40001];

// LIS를 유지하기 위해 숫자가 들어갈 위치를 이분탐색으로 찾는 함수
int binarysearch(int left, int right, int target) {

	int mid;

    // lis 배열에 들어갈 target=arr[i]의 위치를 이분탐색으로 찾기

	while (left < right) {
		mid = (left + right) / 2; // 중간값 설정

		if (lis[mid] < target) {
			left = mid + 1;
		}
		else {
			right = mid;
		}
	}
	return right;
}

int main() {

	ios::sync_with_stdio(0);
	cin.tie(0);

	int n;
	cin >> n;
	for (int i = 0; i < n; i++) {
		cin >> arr[i];
	}

	int j = 0;
	lis[0] = arr[0]; // lis 배열의 맨 첫번째 값은 arr[0]으로 초기화
	int i = 1;

	// arr의 두번째부터 마지막까지 하나씩 lis와 비교하면서 넣어준다.
	while (i < n) {
		// lis 배열의 맨 뒤의 값보다 arr[i]가 더 크면 그것을 lis 배열 맨 뒤에 넣어준다.
		if (lis[j] < arr[i]) {
			lis[j + 1] = arr[i];
			j += 1;
		}
		// arr[i]값이 더 작으면, arr[i]의 값이 lis 배열 중 어느 곳에 들어올지 이분탐색한다.
		else {
            // 0부터 j까지 탐색하면서 arr[i]가 들어갈 수 있는 위치를 찾아서 idx에 반환
			int idx = binarysearch(0, j, arr[i]);
			lis[idx] = arr[i];
		}
		i += 1;
	}

	cout << j + 1;


	return 0;
}

[Python]

# 12015번
import bisect

x = int(input())
arr = list(map(int, input().split()))

dp = [arr[0]]

for i in range(x):
    if arr[i] > dp[-1]:
        dp.append(arr[i])
    else:
        idx = bisect.bisect_left(dp, arr[i])
        dp[idx] = arr[i]

print(len(dp))

---

Reference

LIS (Longest Increasing Subsequence) - 최장 증가 부분 수열

가장 긴 증가하는 부분 수열 (Longest Increasing Subsequence)